
Six Sigma - die neue Zauberformel für Qualität?
Total Quality Management als umfassendes Managementkonzept fasst in Deutschland nur mühsam Fuß. Aber damit ist Schluss, wenn man den Anhängern von Six Sigma Glauben schenken darf. Wer Six Sigma einsetzt, der schafft das Unmögliche: Nur noch drei Fehler bei einer Million produzierter Waren oder erbrachter Dienstleistungen! Aber vor allem: konkret nachgewiesene Einsparungen in einer Höhe, die keine Frage mehr nach den Kosten der Qualität aufkommen lassen. Im ersten Teil dieser Serie erklärt Dr. Georg Angermeier, was Six Sigma bedeutet und was es mit Projektmanagement zu tun hat.
Six Sigma - die neue Zauberformel für Qualität?
Total Quality Management als umfassendes Managementkonzept fasst in Deutschland nur mühsam Fuß. Aber damit ist Schluss, wenn man den Anhängern von Six Sigma Glauben schenken darf. Wer Six Sigma einsetzt, der schafft das Unmögliche: Nur noch drei Fehler bei einer Million produzierter Waren oder erbrachter Dienstleistungen! Aber vor allem: konkret nachgewiesene Einsparungen in einer Höhe, die keine Frage mehr nach den Kosten der Qualität aufkommen lassen. Im ersten Teil dieser Serie erklärt Dr. Georg Angermeier, was Six Sigma bedeutet und was es mit Projektmanagement zu tun hat.
Qualitätsmanagement - das wird als trockene Disziplin außerhalb der Geschäftsprozesse oftmals auf den QM-Beauftragten abgeschoben. Der muss dann für alles, was er (oder sie) tut zuerst einmal die Kosten rechtfertigen. Total Quality Management als umfassendes Managementkonzept fasst in Deutschland nur mühsam Fuß. Aber damit ist jetzt Schluss, wenn man den Anhängern von Six Sigma Glauben schenken darf. Wer Six Sigma einsetzt, der schafft das Unmögliche: Nur noch drei Fehler bei einer Million produzierter Waren oder erbrachter Dienstleistungen! Aber vor allem: konkret nachgewiesene Einsparungen in einer Höhe, die keine Frage mehr nach den Kosten der Qualität aufkommen lassen.
Im ersten Teil soll so einfach wie möglich erklärt werden, was Six Sigma überhaupt bedeutet und was es mit Projektmanagement zu tun hat. In den nächsten Teilen sollen die Meinungen von Experten und Erfahrungsberichte das Bild abrunden.
Genauigkeit und Fehler - ein Beispiel
Nehmen wir als anschauliches Beispiel an, die Zulieferfirma einer Möbelfabrik stellt Kanthölzer mit einer Länge von 200 mm her. Diese Länge darf maximal um 0,3 mm über- oder unterschritten werden. Aufgrund verschiedenster Ursachen (Sägestaub am Anschlag, Dejustierung des Sägeblattes, Ungleichmäßigkeit im Holz, Bedienfehler usw.) unterliegt die Länge der abgesägten Kanthölzer einer scheinbar unvermeidbaren Variation. Diese Variation wird in der Statistik mit dem griechischen Buchstaben Sigma bezeichnet. Nehmen wir an, dass in unserem Beispiel diese statistische Variation 0,1 mm beträgt. Wenn wir nun sehr viele Kanthölzer genau vermessen und jeweils zu Gruppen zusammenfassen, die bis auf ein hundertstel Millimeter gleich lang sind, dann erhalten wir eine so genannte Häufigkeitsverteilung, wie sie in Bild 1 dargestellt ist.
Die Betrachtung der Häufigkeitsverteilung, die den Namen "Gauss'sche Normalverteilung" trägt, liefert uns zwei wichtige Erkenntnisse:
- Nur 68,3 % aller Produkte erfüllen die angegebene Genauigkeitsspezifikation des Prozesses (0,1 mm) tatsächlich. Es gibt stets Produkte, die "aus dem Rahmen fallen."
- Obwohl die Genauigkeit des Prozesses ein Drittel der zulässigen Abweichung berägt, gibt es immer noch Ausschuss und zwar ca. 3 Fehler pro 1000 Produkte.
Wenn das fertige Möbelstück nun aus 100 Einzelteilen besteht und insgesamt 10.000 mal hergestellt wird, dann sind dies eine Million Einzelteile und insgesamt 3000 fehlerhafte Möbelstücke.
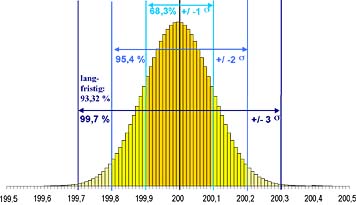
Bild 1: Gauss'sche Normalverteilung um den Mittelwert 200 mit einer Standardabweichung von 0,1
Erschwerend kommt hinzu, dass die langfristige Prozessleistung nochmals erheblich schlechter ist als die kurzfristig gemessene Variation. Aus langjähriger Erfahrung wird bei Six Sigma davon ausgegangen, dass die langfristige Prozessleistung um 1,5 s schlechter ist, als die kurzfristig gemessene. Bei einer kurzfristigen Variation von 3 s bedeutet dies, dass die langfristige Prozessleistung auf 93,32% absinkt bzw. sich 66.807 Fehler bei einer Million Vorgängen ereignen - unter diesen Bedingungen wäre kein einziges Möbelstück wirklich fehlerfrei.
Hier nun setzt Six Sigma an: Das Ziel ist, dass langfristig nur noch 3 Fehler pro einer Million Möglichkeiten (Erfüllung von 99,9997%) auftreten. Konkret heißt dies, dass die kurzfristige Prozessleistung eine Qualität von 6 s (das ist nur noch 1 Fehler pro einer Milliarde Vorgänge!) aufweisen muss, damit die langfristige Leistung eine Qualität von 4,5 s, entsprechend der geforderten 99,9997% zeigt. In Bild 2 wird zur Veranschaulichung dieses extremen Qualitätsziels der rechte Teil der Normalverteilung aus Bild 1 sukzessive herausvergrößert.
Um in der grafischen Darstellung die außerhalb einer Abweichung von 6 s liegenden Werte überhaupt noch darstellen zu können, müssen sie 100.000 fach vergrößert werden!
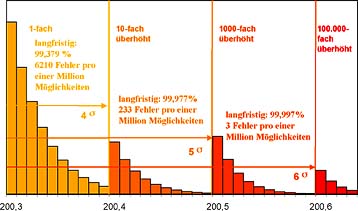
Bild 2: Der rechte Rand der Normalverteilung aus Bild 1, sukkzessive vergrößert, bis zur Grenze von sechs Standardabweichungen (six sigma).









Frank Lehmke
28.02.2016
Dr. Georg Angermeier
29.02.2016
vielen Dank für diesen präzisierenden Hinweis!
Nun ist es nicht Aufgabe des Artikels, die statistischen Feinheiten von Six Sigma exakt darzustellen, sondern die Idee der Methode vorzustellen. Dadurch ist in vielen Punkten, nicht nur bei dem Beispiel mit dem Kantholz, eine grob vereinfachende Darstellung notwendig - man mag gerne auch fehlerhafte Darstellung sagen. So steht im Artikel z.B. ebenfalls nichts über DOE, zweifelsohne ein "Unding", wenn man Six Sigma vollständig darstellen möchte.
Im Text selbst steht übrigens sehr wohl "Fehler pro einer Million Möglichkeiten". Aber Sie haben völlig Recht, dies wird im Beispiel nicht ausgeführt.
Beste Grüße
Georg Angermeier